38) Differential Equations

Last time

• Computing derivatives

• Ill-conditioned optimization

• Recap on Finite Differences

Today

1. Ordinary differential equations (ODE)

2. Explicit methods: Forward Euler method

3. Higher-order time-stepping schemes: Runge-Kutta 4 (RK4)

4. Stability

5. Implicit methods: Backward Euler

using LinearAlgebra
using Plots
default(linewidth=4, legendfontsize=12)
using LaTeXStrings

struct RKTable
    A::Matrix
    b::Vector
    c::Vector
    function RKTable(A, b)
        s = length(b)
        A = reshape(A, s, s)
        c = vec(sum(A, dims=2))
        new(A, b, c)
    end
end

function rk_stability(z, rk)
    s = length(rk.b)
    1 + z * rk.b' * ((I - z*rk.A) \ ones(s))
end

rk4 = RKTable([0 0 0 0; .5 0 0 0; 0 .5 0 0; 0 0 1 0], [1, 2, 2, 1] / 6)
heun = RKTable([0 0; 1 0], [.5, .5])
Rz_theta(z, theta) = (1 + (1 - theta)*z) / (1 - theta*z)

function ode_rk_explicit(f, u0; tfinal=1, h=0.1, table=rk4)
    u = copy(u0)
    t = 0.
    n, s = length(u), length(table.c)
    fY = zeros(n, s)
    thist = [t]
    uhist = [u0]
    while t < tfinal
        tnext = min(t+h, tfinal)
        h = tnext - t
        for i in 1:s
            ti = t + h * table.c[i]
            Yi = u + h * sum(fY[:,1:i-1] * table.A[i,1:i-1], dims=2)
            fY[:,i] = f(ti, Yi)
        end
        u += h * fY * table.b
        t = tnext
        push!(thist, t)
        push!(uhist, u)
    end
    thist, hcat(uhist...)
end

ode_rk_explicit (generic function with 1 method)

1. Ordinary Differential Equations

Given initial condition \(y(t=0)=y(0)=y_0\), we want to find \(y(t)\) for \(t > 0\) that satisfies

\[ y' \equiv \dot y \equiv \frac{\partial y}{\partial t} = f(t, y) \]

Application	\(y\)	\(f\)
Orbital dynamics	position, momentum	conservation of momentum
Chemical reactions	concentration	conservation of atoms
Epidemiology	infected/recovered population	transmission and recovery

• \(y\) can be a scalar or a vector

Solving differential equations

Linear equations

\[ y' = A(t) y + \text{sink}(t)/\text{source}(t)\]

• Autonomous if \(A(t) \equiv A\) and source independent of \(t\): \( y' = A y + \text{sink}/\text{source}\)

• Non-autonomous otherwise

• Suppose \(y\) and \(a = A\) are scalars:

\[ y' = a y\]

then there is an an analytic solution:

\[y(t) = e^{at} y_0\]

• We can do the same for systems

\[ y(t) = e^{A t} y_0 \]

But what does it mean to exponentiate a matrix?

Taylor series again!

\[ e^A = 1 + A + \frac{A^2}{2} + \frac{A^3}{3!} + \dotsb \]

where here \(1\) means the identity matrix \(I\), and there are many practical ways to compute it (a paper co-authored by the founder of MATLAB).

Exponentiate a diagonalizable matrix

Suppose that the diagonalization \(A = X \Lambda X^{-1}\) exists, how do we derive a finite expression for the matrix exponential of \(A\), i.e., \(e^A\), using the scalar exp function?

Solution:

We have:

\[ e^A = 1 + A + \frac{A^2}{2} + \frac{A^3}{3!} + \dotsb \]

\[A^n = (X \Lambda X^{-1})^n = X \Lambda X^{-1} \cdot X \Lambda X^{-1} \cdot X \Lambda X^{-1} \cdot \ldots \cdot X \Lambda X^{-1} = X \Lambda^n X^{-1}\]

Thus,

\[ e^A = X X^{-1} + X \Lambda X^{-1} + X \Lambda^2 X^{-1}/2 + \dots \]

Factoring out the \(X\) and \(X^{-1}\) on the left and right gives:

\[e^A = X (I + \Lambda + \Lambda^2/2 + \dots) X^{-1} = X e^{\Lambda}X^{-1}.\]

Stability of ODEs

A solution of the ODE

\[ y' = f(t, y) \]

is stable if for every \(\varepsilon > 0\) there is a \(\delta > 0\) s. t. if \(\hat y(t)\) satisfies the ODE and \( \hat y(t_0) − y(t_0) \leq \delta\) then \(|| \hat y(t) - y(t)|| \leq \varepsilon\) for all \(t \geq t_0\)

that is, it rules out exponential divergence if initial value is perturbed.

There are different scenarios:

• Asymptotically stable solution: \(|| \hat y(t) - y(t)|| \rightarrow 0 \) as \(t \rightarrow \infty\)

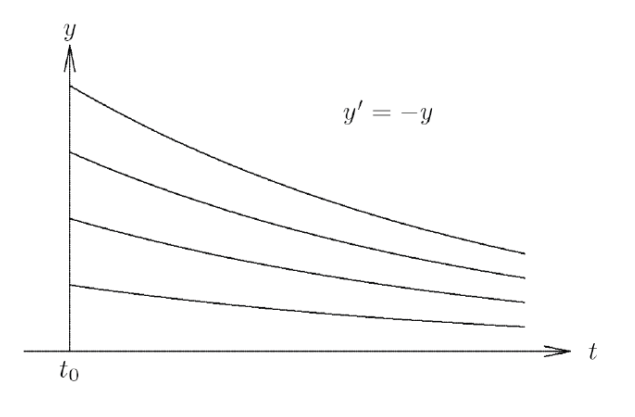
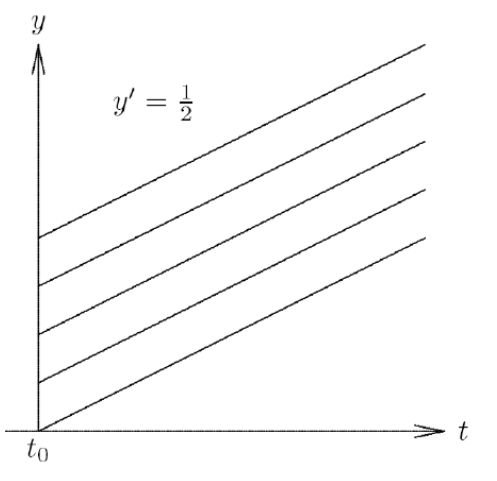
• Stable solution, but not asymptotically so:

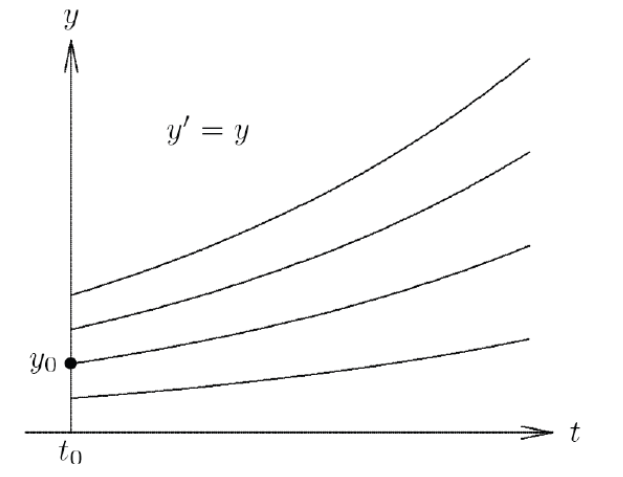
• Unstable solution:

Determining stability

To determine stability of an ODE, we think of the simpler case of a linear, homogenous system \( y' = A y \), or even simpler, where we have only a constant \(\lambda\) multiplied by \(y\). This is called a “test” equation:

\[ y' = \lambda y . \]

We know this has an analytic solution \(y(t) = y_0 e^{\lambda t}\), for an initial condition \(y(0)=y_0\).

• If \(\lambda > 0\), exponential divergence: every solution is unstable.

• \(\lambda < 0\), asymptotical stability: every solution is stable as \(t \rightarrow \infty\).

• If \(\lambda \) is complex:

  • \(e^{\lambda t} = e^{a t} (\cos(b t ) + i \sin( b t))\)

  • \(Re(\lambda) = a\). This is the oscillating component multiplied by a real amplification factor

  • \(Re(\lambda) > 0\): unstable (solution grows)

  • \(Re(\lambda) < 0\): stable (solution decays)

  • \(Re(\lambda) = 0\): oscillating (solution oscillates)

Recap on explicit methods for solving ODEs: Forward Euler method

The simplest method for solving

\[y'(t) = f(t,y)\]

is to use numerical differentiation to approximate the derivative.

Recall: We know the definition of the difference quotient from Calculus:

\[y' = \lim_{h\to 0} \frac{y(t+h) - y(t)}{h}\]

Hence, we can use a forward difference formula:

\[ \frac{\partial {y^n}^F}{\partial t} \approx \frac{ y^{n+1} - y^{n}}{h} + O(h) \equiv \frac{ y^{n+1} - y^{n}}{\Delta t} + O(\Delta t) \]

this is a first-order approximation, where \(h \equiv \Delta t\) is the step size, and we have approximated the time domain (temporal axis) with uniform grid spacing \(\Delta t\), so that \(y^n = n \Delta t\), for \(n = 0, \ldots, N\).

When \(n=0\) we use the initial condition given: \(y(t=0)=y(0)=y_0\)

\[ y' \approx \frac{y(h) - y(0)}{h} \]

which yields

\[ y' \approx \frac{y(h) - y(0)}{h} = f(0, y(0)) \]

Hence, we have the solution estimate

\[ \tilde y(h) = y(0) + h f(0, y(0)) \]

Let’s now use again the simplest linear ODE there exists, the “test” equation:

\[ y' = \lambda y . \]

For \(n=0\) we obtain the solution at new time step (\(n=1\)) knowing all information that is given by the initial condition:

\[ y^{1} = y^0 + h \lambda y^0 , \]

For multiple steps, \((n \geq 1))\), we obtain the recurrence relation:

\[ y^{n+1} = y^n + h \lambda y^n , \]

\[ y^{n+1} = \left(1 + h \lambda \right) y^n . \]

If we apply this repeatedly, we obtain the relation:

\[ y^{n+1} = \left(1 + h \lambda \right)^{n+1} y^0 . \]

Example:

Let’s try this on a scalar problem

\[ y' = -k (y - \cos t) \]

where \(k\) is a parameter controlling the rate at which the solution \(y(t)\) is pulled toward the curve \(\cos t\).

function ode_euler(f, y0; tfinal=10., h=0.1)
    y = copy(y0)
    t = 0.
    thist = [t]
    yhist = [y0]
    while t < tfinal
        tnext = min(t+h, tfinal)
        h = tnext - t
        y += h * f(t, y)
        t = tnext
        push!(thist, t)
        push!(yhist, y)
    end
    thist, hcat(yhist...)
end

ode_euler (generic function with 1 method)

f1(t, y; k=5) = -k * (y .- cos(t))

thist, yhist = ode_euler(f1, [1.], tfinal=10, h=.25)
scatter(thist, yhist[1,:], label = "Forward Euler")
plot!(cos, label = L"\cos(x)")

Forward Euler on a linear system

If we have a system of ODEs:

\[ \dot{\mathbf{y}} = A \mathbf{y} \]

For example, a system of two first-order linear ODEs:

(20)\[\begin{align} y_1' &= y_2\\ y_2' &= - y_1\\ \end{align}\]

In matrix form:

\[\begin{split} \begin{bmatrix} y_1 \\ y_2 \end{bmatrix}' = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \begin{bmatrix} y_1 \\ y_2 \end{bmatrix}\end{split}\]

f2(t, y) = [0 1; -1 0] * y

thist, yhist = ode_euler(f2, [0., 1], h=.02, tfinal=10)
scatter(thist, yhist', label = [L"y_1" L"y_2"])
plot!([cos, sin], label = [L"\cos(x)" L"\sin(x)"])

eigen([0 1; -1 0])

Eigen{ComplexF64, ComplexF64, Matrix{ComplexF64}, Vector{ComplexF64}}
values:
2-element Vector{ComplexF64}:
 0.0 - 1.0im
 0.0 + 1.0im
vectors:
2×2 Matrix{ComplexF64}:
 0.707107-0.0im       0.707107+0.0im
      0.0-0.707107im       0.0+0.707107im

This problem has imaginary eigenvalues (the solution is an oscillator). Forward Euler on this problem is not the best choice: it is amplifying the oscillations!

3. Higher-order time-stepping schemes: Runge-Kutta 4 (RK4)

thist, yhist = ode_rk_explicit(f2, [0., 1], h=0.5, tfinal=10)
scatter(thist, yhist', label = [L"y_1" L"y_2"])
plot!([cos, sin], size=(800, 500), label = [L"\cos(x)" L"\sin(x)"])

• Apparently it is possible to integrate this system using large time steps.

• This method evaluates \(f(t)\) four times per step, so the cost is about equal when the step size \(h\) is 4x larger than forward Euler.

But let’s run it again with a larger step size

thist, yhist = ode_rk_explicit(f2, [0., 1], h=1, tfinal=10)
scatter(thist, yhist', label = [L"y_1" L"y_2"])
plot!([cos, sin], size=(800, 500), label = [L"\cos(x)" L"\sin(x)"])

4. Stability

To analyze stability, we use the Linear Stability Analysis (LSA).

Linear Stability Analysis

Why did Euler diverge (even if slowly) while RK4 solved this problem accurately?

And why do both methods diverge if the step size is too large?

We can understand the convergence of methods by analyzing the test problem

\[ y' = \lambda y \]

for different values of \(\lambda\) in the complex plane.

One step of the Euler method with step size \(h\) maps

\[ y \to y + h \lambda y = \underbrace{(1 + h \lambda)}_{R(h \lambda)} y .\]

For many (\(n \geq 1 \)) steps, we have:

\[ y^{n+1} = y^n + h \lambda y^n . \]

Hence, we obtain the recurrence relation:

\[ y^{n+1} = \underbrace{(1 + h \lambda)}_{R(h \lambda)} y^n, \]

where \(R(h \lambda)\) is called the recurrence relation or growth/amplification factor.

Our solution will stay bounded, that means the numerical scheme is stable if and only if

\[|R(h \lambda)| \leq 1 . \]

Let’s look at examples when this map causes solutions to “blow up” or to be stable.

function plot_stability(Rz, method; xlim=(-3, 2), ylim=(-1.5, 1.5))
    x = xlim[1]:.02:xlim[2]
    y = ylim[1]:.02:ylim[2]
    plot(title="Stability: $method", aspect_ratio=:equal, xlim=xlim, ylim=ylim)
    heatmap!(x, y, (x, y) -> abs(Rz(x + 1im*y)), c=:bwr, clims=(0, 2))
    contour!(x, y, (x, y) -> abs(Rz(x + 1im*y)), color=:black, linewidth=2, levels=[1.])
    plot!(x->0, color=:black, linewidth=1, label=:none)
    plot!([0, 0], [ylim...], color=:black, linewidth=1, label=:none, xlabel = L"Re(\lambda h)", ylabel = L"Im(\lambda h)")
end

plot_stability (generic function with 1 method)

Stability of Forward Euler

plot_stability(z -> 1 + z, "Forward Euler")

This is a complex \(\lambda h \) (or \(\lambda \Delta t\))-plane.

We see that for forward Euler to be numerically stable, we need that \(h \lambda\) must be in the circle of radius \(1\), centered at \(-1\), i.e., for \(\lambda < 0\), it is stable only if \(h \leq -2/\lambda\).

Stability for RK4

plot_stability(z -> rk_stability(4z, rk4), "RK4")

Stability for Heun’s method

plot_stability(z -> rk_stability(2z, heun), "Heun's method")

5. Implicit methods: Backward Euler

Recall that one forward Euler step is

\[ \tilde y(h) = y(0) + h f(0, y(0)) . \]

This can be evaluated explicitly; all the terms on the right hand side are known so the approximation \(\tilde y(h)\) is computed merely by evaluating the right hand side.

Let’s consider an alternative, backward Euler (or “implicit Euler”).

Recall the forward difference formula:

\[ \frac{\partial {y^n}^F}{\partial t} \approx \frac{ y^{n+1} - y^{n}}{h} + O(h) \equiv \frac{ y^{n+1} - y^{n}}{\Delta t} + O(\Delta t) \]

If instead we use the backward difference formula:

\[ \frac{\partial {y^{n}}^B}{\partial t} \approx \frac{ y^{n} - y^{n-1}}{h} + O(h) \equiv \frac{ y^{n} - y^{n-1}}{\Delta t} + O(\Delta t) \]

When \(n=1\) we use the initial condition given: \(y(t=t_0=0)=y(0)=y_0\)

\[ y'(t=t_1) \approx \frac{y(h) - y(0)}{h} \]

which yields

\[ y'(t=t_1) \approx \frac{y(h) - y(0)}{h} = f(t=t_1, y(t=t_1)) \]

which yields to the solution estimate

\[ \tilde y(h) = y(0) + h f(h, \tilde y(h)) . \]

This is a (generally) nonlinear equation for \(\tilde y(h)\).

Stability of backward Euler

For the test equation

\[ \begin{align}\begin{aligned} y' = \lambda y $$, \\at the first time step, the backward Euler method is\\$$ \tilde y(h) = y(0) + h \lambda \tilde y(h), \end{aligned}\end{align} \]

or

\[ \left(1 - h \lambda\right) \tilde y(h) = y(0) , \]

hence

\[ \tilde y(h) = \underbrace{\left( \frac{1}{1 - h \lambda}\right)}_{R(h\lambda)} y(0) . \]

For many steps, \((n \geq 1)\), we obtain:

\[ y^{n+1} = y^n + h \lambda y^{n+1} . \]

Hence, we obtain the recurrence relation:

\[ \left( 1 - h \lambda \right) y^{n+1} = y^n, \]

\[ y^{n+1} = \left( \frac{1}{1 - h \lambda}\right) y^n. \]

If we apply this repeatedly, we obtain:

\[ y^{n+1} ={\underbrace{ \left( \frac{1}{1 - h \lambda } \right)}_{R(h\lambda)}}^{n+1} y^0. \]

We see that to have stability for the Backward Euler scheme we need:

\[ \left| \frac{1}{1 - h \lambda } \right| \leq 1 . \]

plot_stability(z -> 1/(1-z), "Backward Euler")

We can see that the stability region is for \(h \lambda\) anywhere in the left half complex plane, i.e., for any \(h>0\) when \(Re(\lambda)<0\).

• This means that if the problem of interest is stable \(\Rightarrow\) Backward Euler is unconditionally stable, i.e., stable for any positive step size \(h\).

Computing with implicit methods

\[ \tilde y(h) = y(0) + h f\big(\tilde y(h) \big) \]

• Linear solve for linear problem

• Nonlinear (often Newton) solve for nonlinear problem

• Need Jacobian or finite differencing

Stability of midpoint (Crank-Nicolson) scheme

For the test equation

\[y' = \lambda y, \]

one step of the Crank-Nicolson scheme is

\[ \begin{align}\begin{aligned} \frac{y(h) - y(0)}{h} = \frac{1}{2} \left( f( y(0)) + f(y(h)) \right) $$,\\which leads to the solution estimate\end{aligned}\end{align} \]

\tilde y(h) = y(0) + h \frac{1}{2} \left( f( y(0)) + f(\tilde y(h)) \right) . $$

We use the test problem:

\[ \begin{align}\begin{aligned} y' = \lambda y $$, \\and we obtain:\end{aligned}\end{align} \]

\tilde y(h) = y(0) + \frac{h \lambda}{2} y(0) + \frac{h \lambda}{2} \tilde y(h) , $$

which we can rearrange:

\[ \left(1 - \frac{h \lambda}{2} \right) \tilde y(h) = \left(1 + \frac{h \lambda}{2} \right) y(0) , \]

\[ \tilde y(h) = \left(\frac{ 1 + \frac{h \lambda}{2} }{1 - \frac{h \lambda}{2}} \right) y(0) . \]

For many steps, \((n \geq 1)\), we obtain:

\[ y^{n+1} = \left(\frac{ 1 + \frac{h \lambda}{2} }{1 - \frac{h \lambda}{2}} \right) y^n . \]

If we apply this repeatedly, we obtain:

\[ y^{n+1} = {\underbrace{\left(\frac{ 1 + \frac{h \lambda}{2} }{1 - \frac{h \lambda}{2}} \right)}_{R(h\lambda)}}^{n+1} y^0. \]

We see that to have stability for the Crank-Nicolson scheme we need:

\[ \left| \frac{ 1 + \frac{h \lambda}{2} }{1 - \frac{h \lambda}{2}} \right| \leq 1 . \]

plot_stability(z -> Rz_theta(z, .5), "Midpoint (Crank-Nicolson) method")

Again, similarly to the case for Backward Euler, we can see here that the stability region is for \(h \lambda\) anywhere in the left half complex plane, i.e., for any \(h>0\) when \(Re(\lambda)<0\).

• This means that if the problem of interest is stable \(\Rightarrow\) Crank-Nicolson is unconditionally stable, i.e., stable for any positive step size \(h\).