17) Cholesky QR#
Last time#
Householder QR
Today#
Recap on Householder QR
Composition of reflectors
Cholesky Decomposition
Profiling
using LinearAlgebra
using Plots
default(linewidth=4, legendfontsize=12)
function vander(x, k=nothing)
if isnothing(k)
k = length(x)
end
m = length(x)
V = ones(m, k)
for j in 2:k
V[:, j] = V[:, j-1] .* x
end
V
end
function gram_schmidt_classical(A)
m, n = size(A)
Q = zeros(m, n)
R = zeros(n, n)
for j in 1:n
v = A[:,j]
R[1:j-1,j] = Q[:,1:j-1]' * v
v -= Q[:,1:j-1] * R[1:j-1,j]
R[j,j] = norm(v)
Q[:,j] = v / R[j,j]
end
Q, R
end
gram_schmidt_classical (generic function with 1 method)
function reflectors_mult(V, x)
y = copy(x)
for v in reverse(V)
n = length(v) - 1
y[end-n:end] -= 2 * v * (v' * y[end-n:end])
end
y
end
function reflectors_to_dense(V)
m = length(V[1])
Q = diagm(ones(m))
for j in 1:m
Q[:,j] = reflectors_mult(V, Q[:,j])
end
Q
end
reflectors_to_dense (generic function with 1 method)
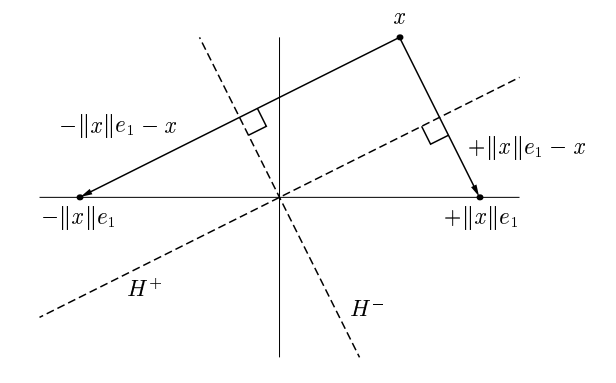
1. Recap on Householder QR#
Householder: An improved algorithm#
function qr_householder(A)
m, n = size(A)
R = copy(A)
V = [] # list of reflectors
for j in 1:n
v = copy(R[j:end, j])
v[1] += sign(v[1]) * norm(v) # <--- here we pick the sign of v so that moves it the largest distance
v = normalize(v)
R[j:end,j:end] -= 2 * v * v' * R[j:end,j:end]
push!(V, v)
end
V, R
end
qr_householder (generic function with 1 method)
A = [1 0; 0 1]
V, R = qr_householder(A)
tau = [2*v[1]^2 for v in V]
@show tau
V1 = [v ./ v[1] for v in V]
@show V1
R
tau = [2.0, 2.0]
V1 = [[1.0, 0.0], [1.0]]
2×2 Matrix{Int64}:
-1 0
0 -1
Householder is backward stable#
m = 40
x = LinRange(-1, 1, m)
A = vander(x, m)
V, R = qr_householder(A)
Q = reflectors_to_dense(V)
@show norm(Q' * Q - I)
@show norm(Q * R - A);
norm(Q' * Q - I) = 5.949301496893686e-15
norm(Q * R - A) = 1.2090264267288813e-14
A = [1 0; 0 1.]
V, R = qr_householder(A) # we don't get NaNs anymore
qr(A) # Julia built-in
LinearAlgebra.QRCompactWY{Float64, Matrix{Float64}, Matrix{Float64}}
Q factor: 2×2 LinearAlgebra.QRCompactWYQ{Float64, Matrix{Float64}, Matrix{Float64}}
R factor:
2×2 Matrix{Float64}:
1.0 0.0
0.0 1.0
Orthogonality is preserved#
x = LinRange(-1, 1, 20)
A = vander(x) # [1 | x | x^2 | ... x^19]
Q, _ = gram_schmidt_classical(A)
@show norm(Q' * Q - I)
v = A[:,end]
@show norm(v)
scatter(abs.(Q[:,1:end-1]' * v), yscale=:log10, title="Classical Gram-Schmidt")
norm(Q' * Q - I) = 1.4985231287367549
norm(v) = 1.4245900685395503
Q = reflectors_to_dense(qr_householder(A)[1])
@show norm(Q' * Q - I)
scatter(abs.(Q[:,1:end-1]' * v), yscale=:log10, title="Householder QR") # they are less linearly dependent, i.e., more linearly independent
norm(Q' * Q - I) = 3.840520021608235e-15
Summary:#
Classic Gram-Schmidt: Usually very poor orthogonality.
Modified Gram-Schmidt: Depends upon condition of \(A\). Fails completely when \(A\) is singular.
Householder triangularization: Always good orthogonality and backward stable.
2. Composition of reflectors#
This turns applying reflectors from a sequence of vector operations to a sequence of (smallish) matrix operations. It’s the key to high performance and the native format (QRCompactWY) returned by Julia qr().
Q, R = qr(A) # Julia built-in
LinearAlgebra.QRCompactWY{Float64, Matrix{Float64}, Matrix{Float64}}
Q factor: 20×20 LinearAlgebra.QRCompactWYQ{Float64, Matrix{Float64}, Matrix{Float64}}
R factor:
20×20 Matrix{Float64}:
-4.47214 0.0 -1.64763 0.0 … -0.514468 2.22045e-16
0.0 2.71448 1.11022e-16 1.79412 -2.498e-16 0.823354
0.0 0.0 -1.46813 5.55112e-17 -0.944961 -2.23779e-16
0.0 0.0 0.0 -0.774796 3.83808e-17 -0.913056
0.0 0.0 0.0 0.0 0.797217 -4.06264e-16
0.0 0.0 0.0 0.0 … -3.59496e-16 0.637796
0.0 0.0 0.0 0.0 -0.455484 -1.3936e-15
0.0 0.0 0.0 0.0 4.40958e-16 -0.313652
0.0 0.0 0.0 0.0 -0.183132 1.64685e-15
0.0 0.0 0.0 0.0 4.82253e-16 0.109523
0.0 0.0 0.0 0.0 … 0.0510878 5.9848e-16
0.0 0.0 0.0 0.0 -2.68709e-15 0.0264553
0.0 0.0 0.0 0.0 -0.0094344 -2.94383e-15
0.0 0.0 0.0 0.0 2.08514e-15 0.00417208
0.0 0.0 0.0 0.0 0.0010525 -2.24994e-15
0.0 0.0 0.0 0.0 … -1.64363e-15 -0.000385264
0.0 0.0 0.0 0.0 -5.9057e-5 7.69025e-16
0.0 0.0 0.0 0.0 1.76642e-16 -1.66202e-5
0.0 0.0 0.0 0.0 -1.04299e-6 -1.68771e-16
0.0 0.0 0.0 0.0 0.0 1.71467e-7
This works even for very nonsquare matrices#
A = rand(1000000, 5)
Q, R = qr(A)
@show size(Q) # this would show you the QRCompactWY format
@show size(Matrix(Q)) # this shows you the actual size of Q, in standard matrix format
@show norm(Q*R - A)
R
size(Q) = (1000000, 1000000)
size(Matrix(Q)) = (1000000, 5)
norm(Q * R - A) = 4.181859677183379e-12
5×5 Matrix{Float64}:
-577.612 -433.412 -433.43 -433.238 -432.724
0.0 -381.792 -163.313 -163.553 -163.387
0.0 0.0 344.701 103.409 103.222
0.0 0.0 0.0 329.253 76.5859
0.0 0.0 0.0 0.0 -320.209
This is known as a “full” (or “complete”) QR factorization, in contrast to a reduced QR factorization in which \(Q\) has the same shape as \(A\).
How much memory does \(Q\) use?
Compare to Python’s numpy.linalg.qr#
Need to decide up-front whether you want full or reduced QR.
Full QR is expensive to represent.
3. Cholesky decomposition#
First some definitions:
A matrix \(A \in \mathbb{R}^{n \times n}\) is symmetric if \(A = A^{T}\) and positive definite if \(x^{T}Ax > 0\) for all nonzero \(x \in \mathbb{R}^n\). Symmetric and positive definite matrices, i.e., symmetric positive definite (SPD) matrices, are the most important class of specially structured matrices that arise in applications.
Intuitively, the largest entry in an SPD matrix is on the diagonal and, more qualitatively, SPD matrices have more “mass” on the diagonal than off the diagonal.
If \(A\) can be factored in a QR-factorization, i.e., \(A = QR\), then we can write:
By applying the transpose of a product, we get:
And since Q is orthogonal (remember: \(QQ^T = Q^TQ =I\)), we get:
If, A is SPD, then it is possible to find a lower triangular matrix \(L\) such that:
Then, we have that
Hence, the lower triangular matrix \(L\) is such that \(L = R^T\) and can be identified as the Cholesky factor of \(A^TA\).
It follows (you can prove it yourself for exercise) that \(Q = A L^{-T}\).
Note: Cholesky decomposition is a special type of a LU decomposition.
We can then solve the normal equations \((A^T A) x = A^T b\), as:
in 2 steps:
First by solving: \(R^T y = A^T b\) for \(y\) via forward-substitution.
Then by solving: \(Rx = y\), via backward-substitution.
function qr_chol(A)
R = cholesky(A' * A).U # using cholesky function from the LinearAlgebra.jl package. The decomposition produces the components L and U.
Q = A / R
Q, R
end
A = rand(10,4) # use a random rectangular matrix
Q, R = qr_chol(A)
@show norm(Q' * Q - I)
@show norm(Q * R - A)
norm(Q' * Q - I) = 9.497292348511781e-16
norm(Q * R - A) = 2.37549462997806e-16
2.37549462997806e-16
x = LinRange(-1, 1, 15)
A = vander(x) # use the Vadermonde matrix
Q, R = qr_chol(A)
@show norm(Q' * Q - I) # really not orthogonal
@show norm(Q * R - A);
norm(Q' * Q - I) = 4.3924133095508784e-5
norm(Q * R - A) = 7.092119431498881e-16
Can we fix this?#
Note that the product of two triangular matrices is triangular.
R = triu(rand(5,5))
R * R
5×5 Matrix{Float64}:
0.81932 0.77297 0.383566 0.481441 1.19
0.0 0.636025 0.90238 1.15553 0.869707
0.0 0.0 0.0750742 0.312202 0.579002
0.0 0.0 0.0 0.247336 0.290351
0.0 0.0 0.0 0.0 0.708143
function qr_chol2(A)
Q, R = qr_chol(A)
Q, R1 = qr_chol(Q)
Q, R1 * R
end
x = LinRange(-1, 1, 15)
A = vander(x) # use the Vadermonde matrix
Q, R = qr_chol2(A)
@show norm(Q' * Q - I) # orthogonal to machine precision now!
@show norm(Q * R - A);
norm(Q' * Q - I) = 9.892569635797733e-16
norm(Q * R - A) = 7.622613303296868e-16
How fast are these methods?#
Let’s do some timing with Julia’s macro @time.
m, n = 5000, 2000
A = randn(m, n)
@time qr(A); # Julia's built-in
0.847167 seconds (7 allocations: 77.393 MiB, 0.48% gc time)
A = randn(m, n)
@time qr_chol(A);
1.016496 seconds (8 allocations: 137.329 MiB, 18.48% gc time)
4. Profiling#
using Pkg
Pkg.add("ProfileSVG")
using ProfileSVG
ProfileSVG.@profview qr(A)
Updating registry at `~/.julia/registries/General.toml`
Resolving package versions...
No Changes to `~/.julia/environments/v1.10/Project.toml`
No Changes to `~/.julia/environments/v1.10/Manifest.toml`