16) Householder QR

16) Householder QR#

Last time#

  • Gram-Schmidt orthogonalization

  • Classical vs Modified Gram-Schmidt

  • QR factorization

Today#

  1. Recap from last time

  2. Householder QR

using LinearAlgebra
using Plots
using Polynomials
default(linewidth=4, legendfontsize=12)

function vander(x, k=nothing)
    if isnothing(k)
        k = length(x)
    end
    m = length(x)
    V = ones(m, k)
    for j in 2:k
        V[:, j] = V[:, j-1] .* x
    end
    V
end

vander (generic function with 2 methods)

1. Recap Gram-Schmidt orthogonalization#

For many applications, we find ourselves interested in the column spaces of a matrix \(A\):

\[ \langle a_1 \rangle \subseteq \langle a_1, a_2 \rangle \subseteq \langle a_1, a_2, a_3 \rangle \ldots \]

The idea of QR factorization is the construction of a sequence of orthonormal vectors, \(q_1, q_2, \ldots\) that span these successive spaces.

Thus, suppose we want to find an orthogonal basis for the span of the columns of \(A\):

\[\begin{split} \Bigg[ a_1 \Bigg| a_2 \Bigg] = \Bigg[ q_1 \Bigg| q_2 \Bigg] \begin{bmatrix} r_{11} & r_{12} \\ 0 & r_{22} \end{bmatrix} \end{split}\]

Given \(a_1, a_2, \dots\), we can construct vectors \(q_1, q_2, \ldots\) and entries \(r_{ij}\), by an iterative process of successive orthogonalization.

Gram-Schmidt with more parallelism#

We are performing the following (from right to left):

(5)#\[\begin{align} w = (I - q_2 q_2^T) (I - q_1 q_1^T) v &= (I - q_1 q_1^T - q_2 q_2^T + q_2 q_2^T q_1 q_1^T) v \\ &= \Bigg( I - \Big[ q_1 \Big| q_2 \Big] \begin{bmatrix} q_1^T \\ q_2^T \end{bmatrix} \Bigg) v \end{align}\]

which can be factored in blocks to expoloit a bit of parallelism. Let’s call this classical Gram-Schmidt.

function gram_schmidt_classical(A)
    m, n = size(A)
    Q = zeros(m, n)
    R = zeros(n, n)
    for j in 1:n
        v = A[:,j]
        R[1:j-1,j] = Q[:,1:j-1]' * v
        v -= Q[:,1:j-1] * R[1:j-1,j]
        R[j,j] = norm(v)
        Q[:,j] = v / R[j,j]
    end
    Q, R
end

gram_schmidt_classical (generic function with 1 method)

m = 20
x = LinRange(-1, 1, m)
A = vander(x, m)
Q, R = gram_schmidt_classical(A)
@show norm(Q' * Q - I) # really not orthogonal; unstable algorithm
@show norm(Q * R - A)

norm(Q' * Q - I) = 1.4985231287367549
norm(Q * R - A) = 

7.350692433565389e-16

7.350692433565389e-16

Classical Vs Modified Gram-Schmidt#

Why does the order of operations matter?#

We are performing the following (from right to left):

(6)#\[\begin{align} w = (I - q_2 q_2^T) (I - q_1 q_1^T) v &= (I - q_1 q_1^T - q_2 q_2^T + q_2 q_2^T q_1 q_1^T) v \\ &= \Bigg( I - \Big[ q_1 \Big| q_2 \Big] \begin{bmatrix} q_1^T \\ q_2^T \end{bmatrix} \Bigg) v \end{align}\]

which can be factored in blocks and is not exact in finite arithmetic.

Let’s look at this a bit more closely. In the classical Gram-Schmidt (CGS), we take each vector, one at a time, and make it orthogonal to all previous vectors. If an error is made in computing \(q_2\) in CGS, so that \(q^T_1q_2=\delta\) is small, but non-zero in finite arithmetic, this will not be corrected for in any of the computations that follow, and it will actually be propagated. In this case, \(v_3\) will not be orthogonal to \(q_1\) or \(q_2\).

Because of rounding errors, in classical Gram-Schmidt, \(Q_{k−1}\) does not have truly orthogonal columns. In modified Gram–Schmidt (MGS) we compute the length of the projection of \(w = v_k\) onto \(q_1\) and subtract that projection (and the rounding errors) from \(w\). Next, we compute the length of the projection of the computed \(w\) onto \(q_2\) and subtract that projection (and the rounding errors) from \(w\), and so on, but always orthogonalizing against the computed version of \(w\).

We can look at the size of what’s left over#

We project out the components of our vectors in the directions of each \(q_j\).

x = LinRange(-1, 1, 23)
A = vander(x)
Q, R = gram_schmidt_classical(A)
scatter(diag(R), yscale=:log10)

The next vector is almost linearly dependent#

x = LinRange(-1, 1, 20)
A = vander(x)
Q, _ = gram_schmidt_classical(A)
#Q, _ = qr(A) # try it with Julia's built-in
v = A[:,end]
@show norm(v)
scatter(abs.(Q[:,1:end-1]' * v), yscale=:log10)

norm(v) = 1.4245900685395503

Right-looking modified Gram-Schmidt#

Each outer step of the modified Gram-Schmidt algorithm can be interpreted as a right-multiplication by a square upper-triangular matrix.

function gram_schmidt_modified(A)
    m, n = size(A)
    Q = copy(A)
    R = zeros(n, n)
    for j in 1:n
        R[j,j] = norm(Q[:,j])
        Q[:,j] /= R[j,j]
        R[j,j+1:end] = Q[:,j]'*Q[:,j+1:end]
        Q[:,j+1:end] -= Q[:,j]*R[j,j+1:end]'
    end
    Q, R
end

gram_schmidt_modified (generic function with 1 method)

m = 20
x = LinRange(-1, 1, m)
A = vander(x, m)
Q, R = gram_schmidt_modified(A)
@show norm(Q' * Q - I) # better, in terms of orthogonality error
@show norm(Q * R - A)

norm(Q' * Q - I) = 8.486718528276085e-9
norm(Q * R - A) = 8.709998074379606e-16

8.709998074379606e-16

Classical versus modified?#

  • Classical

    • Really unstable, orthogonality error of size \(1 \gg \epsilon_{\text{machine}}\)

    • Don’t need to know all the vectors in advance

  • Modified

    • Needs to be right-looking for efficiency

    • Less unstable, but orthogonality error \(10^{-9} \gg \epsilon_{\text{machine}}\)

m = 20
x = LinRange(-1, 1, m)
A = vander(x, m)
Q, R = qr(A) # Julia built-in
@show norm(Q' * Q - I)

norm(Q' * Q - I) = 3.216006485393791e-15

3.216006485393791e-15

2. Householder triangularization#

Householder triangularization is numerically more stable than Gram-Schmidt orthogonaliztion, though it lacks the latter’s applicability as a basis for iterative methods. The Householder algorithm is a process of “orthogonal triangularization”, making a matrix triangular by a sequence of unitary matrix operations.

Gram-Schmidt constructed a triangular matrix \(R\) to orthogonalize \(A\) into \(Q\). Each step was an orthogonal projector, which is a rank-deficient operation.

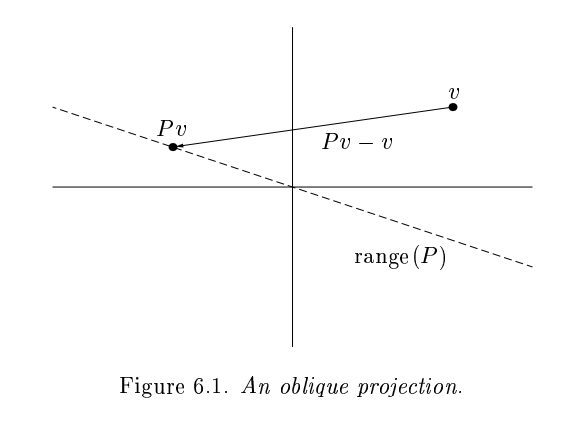
Oblique projector (Trefethen and Bau, 1999)

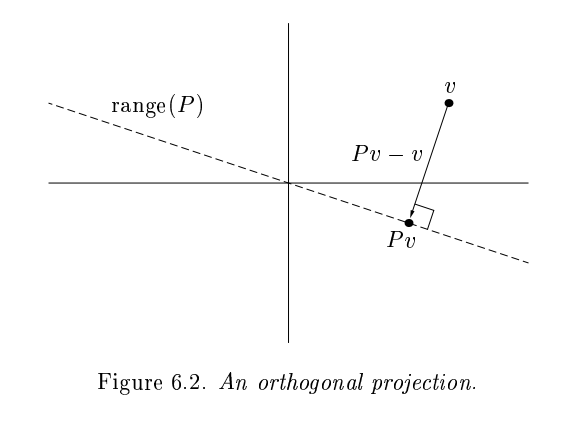
Orthogonal projector (Trefethen and Bau, 1999)

Householder uses orthogonal transformations (reflectors) to triangularize.

\[ \underbrace{Q_{n} \dotsb Q_1}_{Q^T} A = R \]

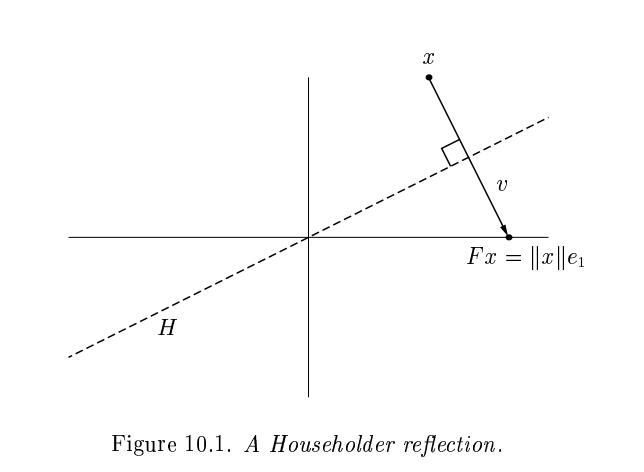
Householder Reflector (Trefethen and Bau, 1999)

The reflection, as depicted above by Trefethen and Bau (1999) can be written \(F = I - 2 \frac{v v^T}{v^T v}\).

The structure of the algorithm is

\[\begin{split} \underbrace{\begin{bmatrix} * & * & * \\ * & * & * \\ * & * & * \\ * & * & * \\ * & * & * \\ \end{bmatrix}}_{A} \to \underbrace{\begin{bmatrix} * & * & * \\ 0 & * & * \\ 0 & * & * \\ 0 & * & * \\ 0 & * & * \\ \end{bmatrix}}_{Q_1 A} \to \underbrace{\begin{bmatrix} * & * & * \\ 0 & * & * \\ 0 & 0 & * \\ 0 & 0 & * \\ 0 & 0 & * \\ \end{bmatrix}}_{Q_2 Q_1 A} \to \underbrace{\begin{bmatrix} * & * & * \\ 0 & * & * \\ 0 & 0 & * \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}}_{Q_3 Q_2 Q_1 A} \end{split}\]

Constructing the \(Q_j\)#

\[ \underbrace{Q_{n-1} \dotsb Q_0}_{Q^T} A = R \]

Each of our \(Q_j\) will have the form

\[\begin{split}Q_j = \begin{bmatrix} I_j & 0 \\ 0 & F \end{bmatrix}\end{split}\]
where \(F\) is a “reflection” that achieves
\[\begin{split} F x = \begin{bmatrix} \lVert x \rVert \\ 0 \\ 0 \\ \vdots \end{bmatrix} \end{split}\]
where \(x\) is the column of \(R\) from the diagonal down. This transformation is a reflection across a plane with normal \(v = Fx - x = \lVert x \rVert e_1 - x\).

The two methods can be summarized as follows:

  • Gram-Schmidt: a triangular orthogonalization

  • Householder: an orthogonal triangularization

Adventures in reflection#

A = rand(4, 4); A += A'
v = copy(A[:,1])
@show norm(v)
v[1] -= norm(v)
v = normalize(v)
F = I - 2 * v * v'
B = F * A # we have zeroed-out all entries below the diagonal in the first column

norm(v) = 2.2766747852711893

4×4 Matrix{Float64}:
  2.27667       2.19264    1.54439    2.40011
 -2.88354e-16  -0.178057   0.191334  -0.45704
 -1.4428e-16   -0.623657  -0.514409  -0.902893
 -3.65367e-16  -1.03764   -0.419731  -0.410995

v = copy(B[2:end, 2])
v[1] -= norm(v)
v = normalize(v)
F = I - 2 * v * v'
B[2:end, 2:end] = F * B[2:end, 2:end] # we have zeroed-out all entries below the diagonal also in the 2nd column
B

4×4 Matrix{Float64}:
  2.27667       2.19264       1.54439    2.40011
 -2.88354e-16   1.22366       0.590258   0.875193
 -1.4428e-16   -5.55112e-17  -0.336919  -0.310152
 -3.65367e-16   0.0          -0.124423   0.575206

Householder: A naive algorithm#

function qr_householder_naive(A)
    m, n = size(A)
    R = copy(A)
    V = [] # list of reflectors
    for j in 1:n
        v = copy(R[j:end, j])
        v[1] -= norm(v)
        v = normalize(v)
        R[j:end,j:end] -= 2 * v * (v' * R[j:end,j:end])
        push!(V, v)
    end
    V, R
end

qr_householder_naive (generic function with 1 method)

m = 4
x = LinRange(-1, 1, m)
A = vander(x, m)
V, R = qr_householder_naive(A)
_, R_ = qr(A)
R_

4×4 Matrix{Float64}:
 -2.0  0.0      -1.11111      0.0
  0.0  1.49071   1.38778e-17  1.3582
  0.0  0.0       0.888889     9.71445e-17
  0.0  0.0       0.0          0.397523

How to interpret \(V\) as \(Q\)?#

The following two programs compute a matrix containing vectors that generate the Householder reflectors whose product is Q.

function reflectors_mult(V, x)
    y = copy(x)
    for v in reverse(V)
        n = length(v) - 1
        y[end-n:end] -= 2 * v * (v' * y[end-n:end])
    end
    y
end

function reflectors_to_dense(V)
    m = length(V[1])
    Q = diagm(ones(m))
    for j in 1:m
        Q[:,j] = reflectors_mult(V, Q[:,j])
    end
    Q
end

reflectors_to_dense (generic function with 1 method)

m = 20
x = LinRange(-1, 1, m)
A = vander(x, m)
V, R = qr_householder_naive(A)
Q = reflectors_to_dense(V)
@show norm(Q' * Q - I)
@show norm(Q * R - A);

norm(Q' * Q - I) = 3.7994490775439526e-15
norm(Q * R - A) = 7.562760794606217e-15

Great, but we can still break it#

A = [1. 0; 0 1.] # identity matrix, with canonical basis vectors in columns
V, R = qr_householder_naive(A)

(Any[[NaN, NaN], [NaN]], [NaN NaN; NaN NaN])

We had the lines

    v = copy(R[j:end, j])
    v[1] -= norm(v)
    v = normalize(v)

What happens when R is already upper triangular?

In this case

\[\begin{split}v = \begin{bmatrix}1 \\ 0 \end{bmatrix} \end{split}\]

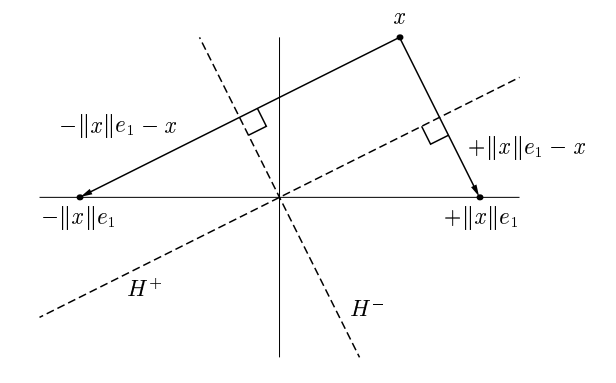
Choosing the better of two Householder reflectors (Trefethen and Bau, 1999).

In general, there are two possible reflections. For numerical stability, it is important to choose the one that moves \(x\) the largest distance, so that it is not too close to \(x\) itself.

In fact, suppose that in the above figure, the angle of \(H^{+}\) and the \(e_1\) axis is much smaller than \(x\) or \(|| x || e_1\). Thus, the calculation of \(v\) represents a subtraction of nearby quantities and will tend to suffer from cancellation errors. We can pick the sign of \(v\) so that we can avoid such effects by ensuring that \(||v||\) is never smaller than \(||x||\).

Householder: An improved algorithm#

function qr_householder(A)
    m, n = size(A)
    R = copy(A)
    V = [] # list of reflectors
    for j in 1:n
        v = copy(R[j:end, j])
        v[1] += sign(v[1]) * norm(v) # <--- here we pick the sign of v so that moves it the largest distance
        v = normalize(v)
        R[j:end,j:end] -= 2 * v * v' * R[j:end,j:end]
        push!(V, v)
    end
    V, R
end

qr_householder (generic function with 1 method)

A = [1 0; 0 1]
V, R = qr_householder(A)
tau = [2*v[1]^2 for v in V]
@show tau
V1 = [v ./ v[1] for v in V]
@show V1
R

tau = [2.0, 2.0]
V1 = 

[[1.0, 0.0], [1.0]]

2×2 Matrix{Int64}:
 -1   0
  0  -1

Householder is backward stable#

m = 40
x = LinRange(-1, 1, m)
A = vander(x, m)
V, R = qr_householder(A)
Q = reflectors_to_dense(V)
@show norm(Q' * Q - I)
@show norm(Q * R - A);

norm(Q' * Q - I) = 5.949301496893686e-15
norm(Q * R - A) = 1.2090264267288813e-14

A = [1 0; 0 1.]
V, R = qr_householder(A) # we don't get NaNs anymore
qr(A) # Julia built-in

LinearAlgebra.QRCompactWY{Float64, Matrix{Float64}, Matrix{Float64}}
Q factor: 2×2 LinearAlgebra.QRCompactWYQ{Float64, Matrix{Float64}, Matrix{Float64}}
R factor:
2×2 Matrix{Float64}:
 1.0  0.0
 0.0  1.0

Orthogonality is preserved#

x = LinRange(-1, 1, 20)
A = vander(x) # [1 | x | x^2 | ... x^19]
Q, _ = gram_schmidt_classical(A)
@show norm(Q' * Q - I)
v = A[:,end]
@show norm(v)
scatter(abs.(Q[:,1:end-1]' * v), yscale=:log10, title="Classical Gram-Schmidt")

norm(Q' * Q - I) = 1.4985231287367549
norm(v) = 1.4245900685395503

Q = reflectors_to_dense(qr_householder(A)[1])
@show norm(Q' * Q - I)
scatter(abs.(Q[:,1:end-1]' * v), yscale=:log10, title="Householder QR") # they are less linearly dependent, i.e., more linearly independent

norm(Q' * Q - I) = 3.840520021608235e-15

Summary:#

  • Classic Gram-Schmidt: Usually very poor orthogonality.

  • Modified Gram-Schmidt: Depends upon condition of \(A\). Fails completely when \(A\) is singular.

  • Householder triangularization: Always good orthogonality and backward stable.

Contents